
Occorre fare dapprima una premessa sulla capacità portante dei pali. Nella fase di progettazione di una fondazione profonda, il carico ultimo e i cedimenti conseguenti sono grandezze tra loro interdipendenti.
L’andamento delle curve sforzi-deformazioni, osservate da prove di carico effettuate su pali singoli, ha permesso di riconoscere tre principali comportamenti all’aumentare del carico che simulano il comportamento del palo in esercizio: una prima fase di deformazione elastica, corrispondente al tratto rettilineo iniziale della curva, una successiva fase deformazione di tipo elasto-plastico, evidenziata dall’andamento curvilineo, e un ultimo tratto a comportamento plastico, in cui si osserva nuovamente un andamento lineare nella curva. Quest’ultimo tratto è normalmente caratterizzato da coefficiente di proporzionalità piuttosto elevato, il che significa che per lievi incrementi di carico si osservano cedimenti significativi.
La condizione di carico più frequente per un palo di fondazione è il carico assiale (verticale) di compressione; la progettazione richiede pertanto la determinazione del carico limite di rottura del palo sotto l’azione dei carichi verticali.
Pertanto, lo scopo è determinare il carico limite Qlim ovvero la capacità portante ultima (ovvero quel carico che applicato alla testa del palo produce la rottura del terreno posto al di sotto della punta del palo e/o lungo la sua superficie laterale (ovvero lungo il fusto del palo) che costituisce un limite superiore oltre il quale si ha il collasso del meccanismo palo-terreno. Per la determinazione della Qlim vi sono diversi criteri che si possono suddividere in due metodi principali:
- metodo analitico (detto anche semi-empirico per la presenza di numerosi coefficienti semi-empirici di correzione) basato sull’utilizzo di formule statiche (diverse per Autori diversi a seconda di alcune ipotesi assunte ed esprimono il carico limite in funzione della geometria del palo e delle caratteristiche del terreno e dell’interfaccia palo-terreno, consentono di esprimere in modo analitico il comportamento a rottura del terreno
- metodo empirico basato essenzialmente su prove di carico su pali pilota (prototipi di pali di varia grandezza).
Altro metodo ancora è quello basato sui risultati di prove penetrometriche statiche e dinamiche possono essere correlati alle resistenze unitarie alla punta e lungo il fusto del palo.
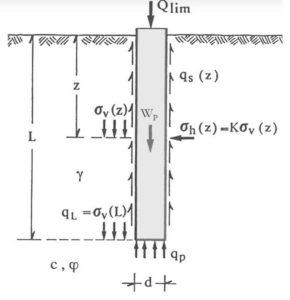
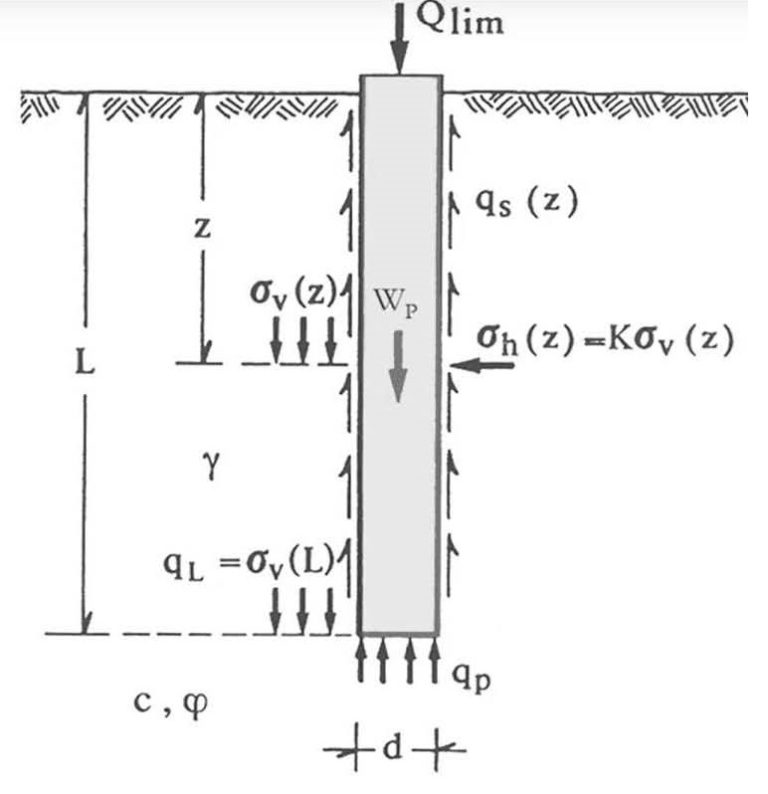
La Qlim determinata per via analitica (formula statica) è data dalla somma di due contributi calcolati separatamente: la resistenza di punta del palo (portata limite mobilitata alla punta) Qp a cui si somma quella laterale (portata limite mobilitata sulla superficie laterale) = Qs a cui va sottratto il peso proprio del palo Wp. Quindi
Qlim = Qp + Qs – Wp
La suddivisione tra QP e QS è convenzionale in quanto le resistenze alla punta e laterali non vengono mobilitate per uno stesso valore del cedimento del palo.
I risultati sperimentali mostrano che la resistenza laterale raggiunge il suo valore limite per cedimenti del palo di 5 ÷ 10 mm circa, indipendentemente dal diametro del palo, mentre la resistenza alla punta si mobilita solo dopo cedimenti dell’ordine del 10 % del diametro per i pali battuti e del 25 % del diametro per i pali trivellati. Nel calcolo di QP e QS si prescinde inoltre dalla interferenza tra i due fenomeni di rottura.
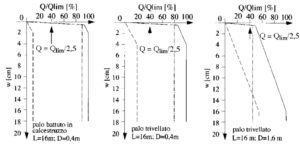
Nella seguente figura tratta da Viggiani (1999) sono diagrammati i valori della resistenza laterale e alla punta per diversi tipi di palo in funzione del cedimento.
Esaminando la figura, si osserva che:
– un palo di 40 cm di diametro, battuto o trivellato, (prime due figure di sinistra) esibisce una resistenza alla punta (linea tratteggiata) assai ridotta rispetto a quella laterale (linea con tratto-punto). In corrispondenza del carico di esercizio (il carico massimo ammissibile è dato da Qlim/2.5 (avendo assunto 2.5 come fattore di sicurezza) corrispondente nel grafico a Q/Qlim = 40% come mobilitazione di Q complessiva), l’aliquota di resistenza alla punta che è operativa risulta modesta anche se il margine di sicurezza complessivo del palo non ne risulta significativamente influenzato. Si osservi come la resistenza laterale (molto maggiore come aliquota rispetto a quella alla punta) sia quasi completamente mobilitata;
– un palo trivellato di grande diametro (1,6 m di diametro) invece, si osserva che la resistenza alla punta rappresenta un’aliquota significativa del carico limite ed è evidente che in corrispondenza del carico di esercizio = Qlim/2.5, la resistenza laterale è completamente mobilitata e i cedimenti che mobilitano la resistenza alla punta sono talmente alti da equivalere in pratica ad una vera e propria rottura.
Per i motivi sopra esposti si avrà che:
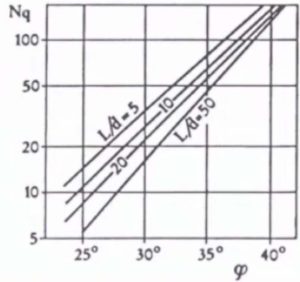
- per pali di medio diametro la determinazione della resistenza alla punta può essere calcolata secondo la teoria di Berezantsev (1961) dove il valore di Nq si ricava per via tabellare, entrando nel grafico con il valore L/D (rapporto lunghezza diametro del palo) e con l’angolo di attrito di calcolo fc definito come:
fc = f-3° per i pali trivellati
fc = (f+40°)/2 per i pali battuti
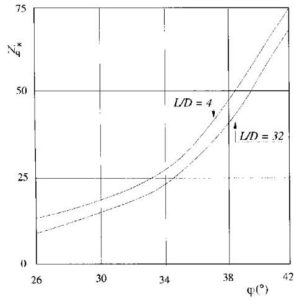
- la valutazione della resistenza alla punta dei pali trivellati di grande diametro, invece, deve essere basata su considerazioni relative ai cedimenti ammissibili, piuttosto che alla rottura alla base del palo stesso. Il progetto dei pali di grande diametro viene pertanto basato essenzialmente sulla considerazione di uno stato limite di servizio. Pertanto, per pali di grande diametro, Berezantsev (1965) propone di utilizzare nel progetto il valore dello sforzo alla punta in corrispondenza del quale si verificano nel terreno le prime deformazioni plastiche. Tale sforzo, che provocherebbe cedimenti compresi tra 0.06 e 0.1 volte il diametro del palo, ovvero del 6-10%D; nel caso di terreni incoerenti suggerisce quindi di introdurre un coefficiente di riduzione Nq* che tiene conto di questo fenomeno di completa plasticizzazione (si veda l’immagine seguente tratta da Viggiani, 1999) e che corrisponde a valori ridotti di Nq.