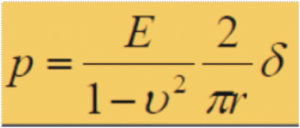Nella progettazione di pavimentazioni, nel controllo in corso d’opera e in fase di collaudo le prove di portanza del sottofondo (capacità portante), siano esse effettuate in situ o in laboratorio, rappresentano delle indagini essenziali per la valutazione della misura di rigidità e della corretta realizzazione della pavimentazione.

Prova CBR
Nel caso delle prove di laboratorio, le indagini per la misura della portanza del sottofondo sono rappresentate dalle prove CBR (California Bearing Ratio), attraverso la determinazione del cosiddetto Indice CBR, mentre in situ esse sono rappresentate dalle prove di carico su piastra, attraverso le quali è possibile determinare il cosiddetto modulo di reazione di sottofondo con il metodo di Westergaard.
Oltre al modello proposto da Westergaard è possibile ricorrere a quello di Boussinesq: entrambi i modelli restituiscono un valore di portanza calcolato sulla base di prove di carico su piastra circolare rigida.
Nel modello di Boussinesq, il sottosuolo è assimilato a un semispazio elastico lineare omogeneo e isotropo dove il parametro di portanza è rappresentato dal modulo elastico E e dal rapporto (o coefficiente) di Poisson ν. Il legame tra la pressione p e il cedimento δ ottenuto con la prova di carico su piastra circolare rigida (con diametro inferiore a 76 cm, in genere compreso tra 16 e 45 cm) è dato dalla formula:
dove:
ν è il coefficiente di Poisson. Esso generalmente vale 0,35-0,40 per terreni granulari (ghiaie e sabbie) e 0,50 per terreni fini (limi e argille);
r è il raggio della piastra;
E è il modulo elastico (o di elasticità o di Young);
δ corrisponde alla deformazione, la cui valutazione può essere fatta o inserendo il valore del cedimento ottenuto al I ciclo di carico, o a quello ottenuto al II ciclo di carico, al cedimento ottenuto al X ciclo di carico o ancora, al cedimento dovuto alla sola componente elastica della deformazione (ovvero alla differenza tra la deformazione totale e quella plastica). E’ necessario ora specificare che il cedimento δ prodotto dal carico applicato alla piastra quando il carico viene rimosso, vi è una componente plastica della deformazione δp (cedimento plastico) che rimane e una componente elastica δe che viene restituita. Nel grafico rappresentante i cicli di carico ripetuti si osserva che la deformazione plastica (fp nel grafico) per ciascun ciclo si riduce, mentre quella elastica (fe nel grafico) rimane costante.
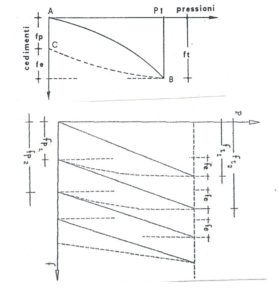
Prova di carico a ciclo unico (sopra) e a cicli ripetuti (sotto). Nel grafico f corrisponde a δ.
Nel modello di Westergaard, invece, il terreno è assimilato a un mezzo elastico e lineare dove il cedimento puntuale dipende solo dal carico applicato: la portanza delle pavimentazioni è quindi rappresentata da un coefficiente K, detto modulo di reazione o costante di reazione del sottofondo [kg/cm3 o MPa/m o daN/cm3]. Esso è quindi definito dal rapporto tra le pressioni che si scaricano sul terreno e le corrispondenti deformazioni. Per l’impostazione del carico è quindi prescritto l’utilizzo di una piastra circolare rigida da 76 cm di diametro caricata una sola volta (prova di carico a ciclo unico), trasmettendo al sottofondo una pressione di 0,70 kg/cm2 e si misura il rapporto tra questa pressione e il cedimento della piastra. Utilizzando quindi piastra di grande diametro (non inferiore a 76 cm) i cedimenti δ risultano proporzionali alle pressioni p. Il rapporto tra pressione e cedimento corrisponde alla costante di reazione del sottofondo (modello di Westergaard)
Il modello di Westergaard si presta bene allo studio dei sottofondi quando i carichi sono trasmessi da superfici molto grandi come quelle delle lastre in calcestruzzo.
La normativa CNR BU n. 92 del 1983 stabilisce l’utilizzo della piastra da 76 cm e la misura dei cedimenti in corrispondenza di una pressione di precarico di 0,1 kg/cm2 e un valore finale di 0,8 kg/cm2.
Ovvero, K = Δp/ Δs = (0,8-0,1) kg/cm2/(s2-s1) cm = 0,7 kg/cm2/(s2-s1) cm, essendo s2 il cedimento relativo alla pressione 0,8 kg/cm2 e s1 il cedimento relativo alla pressione di 0,1 kg/cm2.
Valori indicativi di K sono i seguenti:
K = 9-20 kg/cm3 per terreni A1 e A3
K = 5-15 kg/cm3 per terreni A2
K = 1,5 – 6 per terreni A4, A5, A6 e A7
In conclusione, si può affermare che il cedimento cresce con il diametro della piastra, fino a quando non si raggiunge il valore di 76 cm. Oltre questo diametro il cedimento si mantiene costante (si veda il grafico seguente). La piastra da 76 cm di dimetro corrisponde in ascissa al valore 0,05 mentre una piastra da 30 cm di diametro corrisponde in ascissa al valore di 0,13.
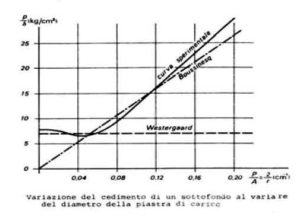
Modelli elastici utilizzati per modellare il sottofondo. In ascisse il rapporto P/A (perimetro/area della piastra) e in ordinate il rapporto pressione-cedimenti.
La retta di Boussinesq passante per l’origine che bene approssima il tratto ascendente della curva sperimentale. L’intersezione della retta di Boussinesq e quella orizzontale di Westergaard corrisponde al raggio di 38 cm (ovvero piastra da 76 cm di diametro). Per diametro inferiore a 76 cm il cedimento si deduce dal semispazio elastico (modello di Boussinesq); per diametri maggiori il cedimento è indipendente dal diametro della piastra.
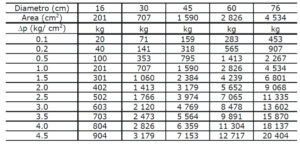
Infine, si riporta una tabella relativa alla forza da applicare (in kg) (ovvero il contrasto) a piastre di diverso diametro per ottenere gli incrementi di pressione Δp richiesti dalla prova.
In conclusione, se si assume un sottofondo a un semispazio elastico, omogeneo, isotropo, ovvero pavimentazione flessibile o semirigida (modello di Boussinesq) si dovrà usare una piastra con diametro inferiore a 76 cm; se invece si utilizza il modello di Westergaard (modello elastico lineare), ovvero pavimentazioni rigide, la portanza dovrà essere misurata con piastre con diametro non inferire a 76 cm.